Introduzione
Il mondo della matematica spesso si intreccia con la vita di tutti i giorni in modi sorprendenti e affascinanti. Un esempio iconico di questo intreccio è il concetto topologico che lega una tazza da caffè e un ciambellone. Ma come può una disciplina matematica così avanzata come la topologia avere qualcosa a che fare con il nostro quotidiano caffè mattutino?
La Magia della Topologia
La topologia, spesso descritta come “geometria gommosa”, è una branca della matematica che trascende le rigide restrizioni della geometria euclidea, concentrandosi invece sulle proprietà degli spazi che persistono attraverso le deformazioni. Mentre la geometria classica potrebbe chiedersi della lunghezza di un lato di un triangolo o dell’angolo tra due linee, la topologia è interessata a concetti molto più flessibili e universali.
Equivalenza Topologica
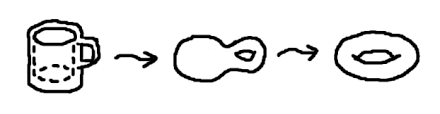
Uno dei concetti centrali della topologia è l’idea di equivalenza topologica. Due oggetti sono considerati topologicamente equivalenti se possono essere deformati l’uno nell’altro senza l’uso di tagli o incollaggi. Questo significa che possono essere stirati, compressi o piegati in ogni modo possibile, ma non possono essere strappati o incollati insieme in punti diversi. Questo concetto porta a intuizioni sorprendenti, come l’idea che un ciambellone e una tazza siano topologicamente equivalenti a causa della loro singola “lacuna”.
Classificazione degli Spazi
Un’applicazione fondamentale della topologia è la classificazione degli spazi in base alle loro proprietà. Ad esempio, gli spazi possono essere distinti in base al numero di “buchi” o “lacune” che possiedono. Una sfera, che non ha buchi, è topologicamente diversa da un ciambellone, che ha un buco. Allo stesso modo, un ciambellone è diverso da una ciambella con due buchi. Questa capacità di classificare e distinguere tra vari spazi è fondamentale in molte applicazioni, dalla fisica alla biologia.
Invarianti Topologici
Un altro aspetto chiave della topologia è la ricerca di invarianti topologici, che sono proprietà o numeri associati a uno spazio che non cambiano sotto deformazioni continue. Questi invarianti aiutano i matematici a classificare e studiare spazi da una prospettiva topologica. Un esempio classico è il “numero di genere”, che indica il numero di buchi in una superficie.
Connettività e Complessità
La topologia esplora anche concetti come la connettività, ossia come le parti di uno spazio sono collegate tra loro. Questo ha importanti applicazioni in aree come la teoria delle reti, dove la struttura e la connessione tra nodi e link possono essere descritte usando strumenti topologici. Inoltre, affronta la complessità degli spazi, cercando di comprendere la struttura intrinseca e le relazioni tra diverse parti di uno spazio.
In sintesi, la topologia è veramente magica nella sua capacità di vedere oltre le apparenze superficiali e di svelare le proprietà fondamentali e universali degli spazi. Con la sua flessibilità e profondità, ha rivoluzionato la nostra comprensione della matematica e del mondo fisico.
Dal Ciambellone alla Tazza di Caffè
Ecco dove entra in gioco la nostra tazza da caffè e il ciambellone. Immagina di avere un ciambellone di plastica elastica. Se iniziassi a deformarlo, potresti “allungare” la parte centrale del ciambellone per formare un manico, mentre “comprimi” il resto per formare il corpo di una tazza. Questo processo di deformazione dimostra che, dal punto di vista topologico, una tazza da caffè e un ciambellone sono equivalenti. Entrambi hanno un singolo “buco” – il centro del ciambellone o il manico della tazza.
Oltre la Tazza: L’Importanza della Topologia
Mentre l’analogia della tazza e del ciambellone può sembrare un trucco matematico divertente, la topologia ha applicazioni molto più ampie e profonde. È fondamentale in fisica, in particolare nella teoria delle stringhe e nella meccanica quantistica. Anche nell’era digitale, la topologia trova applicazione nell’analisi dei dati e nella comprensione delle reti complesse. Il concetto di “invarianza topologica” ha aiutato gli scienziati a comprendere meglio le proprietà fondamentali dell’universo e delle strutture complesse che lo compongono.
La Topologia nella Vita Quotidiana
Mentre la topologia può sembrare un campo esotico e lontano dalla vita di tutti i giorni, in realtà, ha implicazioni in molte aree. Ad esempio, la teoria delle reti, che è fondamentale per la comprensione di Internet e delle reti sociali, si basa su principi topologici. Anche le lezioni di matematica online spesso trattano argomenti di topologia, rendendola accessibile a chiunque attraverso piattaforme come https://www.math4you.online/. Grazie alla topologia, possiamo guardare il mondo attorno a noi in modi nuovi e sorprendenti, riconoscendo le connessioni invisibili tra oggetti e concetti apparentemente disconnessi.
Conclusione
La topologia ci offre una prospettiva unica sulla matematica e sul mondo che ci circonda. Che si tratti di vedere la relazione tra una tazza di caffè e un ciambellone o di comprendere le connessioni profonde all’interno di una rete complessa, la topologia ci sfida a guardare oltre l’ovvio e a riconoscere le verità nascoste nella struttura e nella forma.